Transforming normal to uniform distribution
Problem
Given a random variable \(X \sim \mathcal{N}(\mu,\sigma^2)\), find a transformation \(f: X \rightarrow Y\), such that \(Y \sim Uniform(a,b)\).
Solution
Let \(\Phi_X(\cdot)\) the cumulative distribution function of \(X\).
\[ \begin{eqnarray} Z \equiv \frac{X - \mu}{\sigma};\quad Z &\sim& \mathcal{N}(0;1) \\ \Phi_{Z}\left(\frac{X-\mu}{\sigma}\right) &\sim& Uniform(0;1) \\ (b-a) \Phi_{Z}\left(\frac{X-\mu}{\sigma}\right) &\sim& Uniform(0,b-a) \\ a + (b-a) \Phi_{Z}\left(\frac{X-\mu}{\sigma}\right) &\sim& Uniform(a,b) \end{eqnarray} \]
In conclusion, \(Y \equiv a + (b-a) \Phi_X\left(\frac{X-\mu}{\sigma}\right)\).
Computational demonstration
norm2unif = function(x, mu = 0, sigma = 1, min = 0, max = 1, use.empirical.mean = FALSE, use.empirical.sd = FALSE) {
if (use.empirical.mean) mu = mean(x)
if (use.empirical.sd) sigma = sd(x)
x_std = (x-mu)/sigma
x_std.cdf = ecdf(x_std) # the empirical cumulative distribution function of standardized x
return((max-min)*x_std.cdf(x_std) + min)
}Using exact parameters
Standard distributions
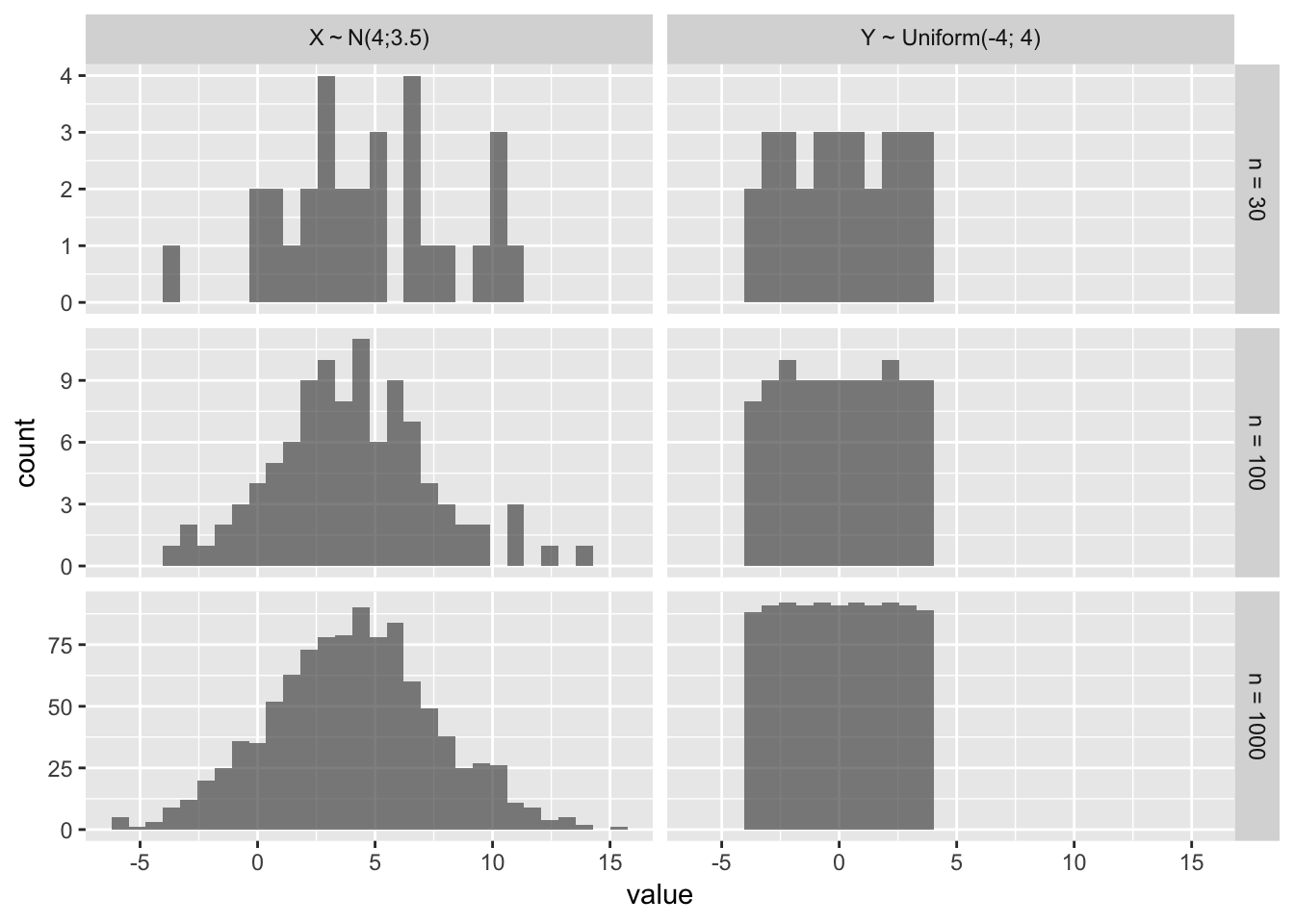
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.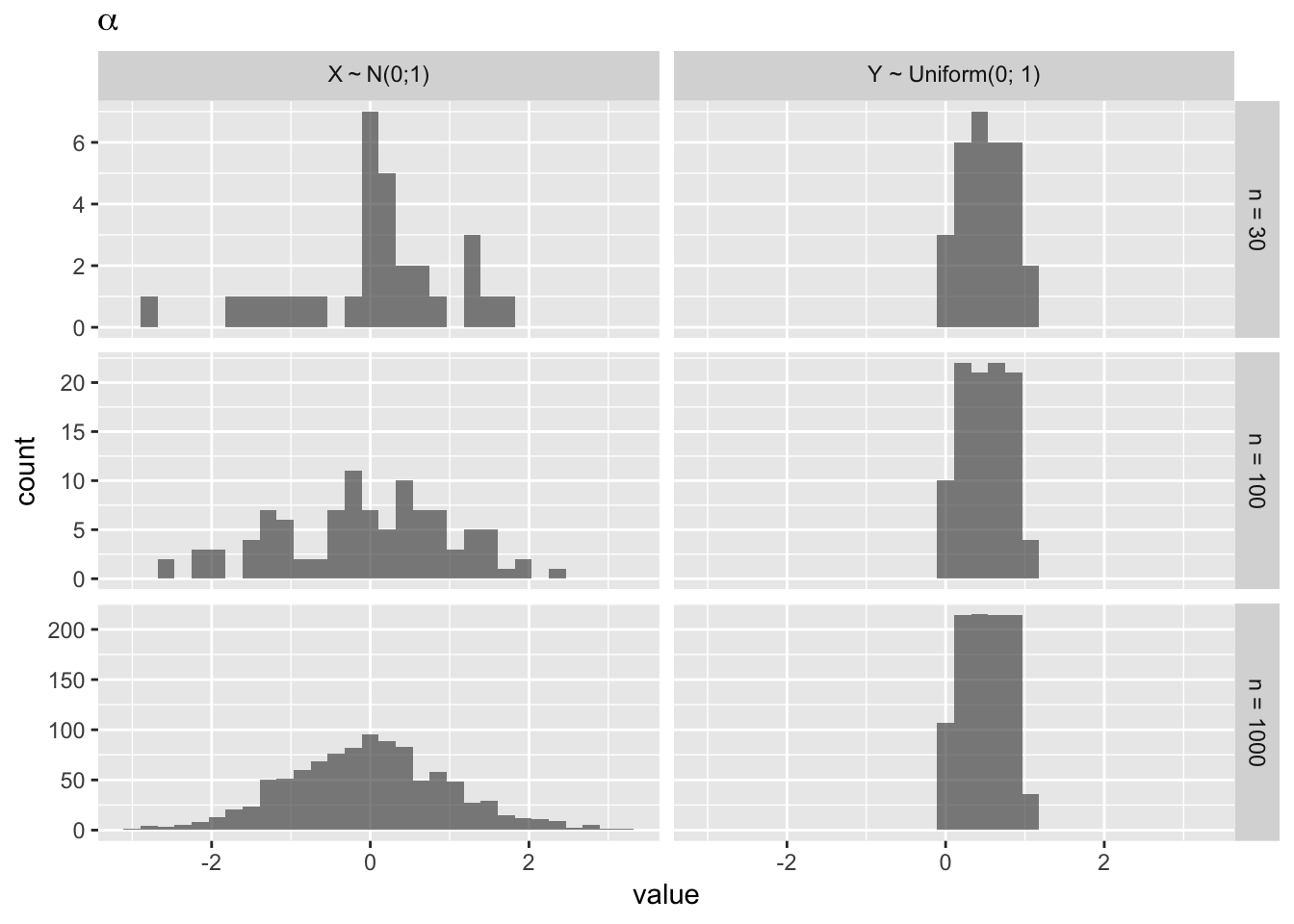
Non-standard distributions
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.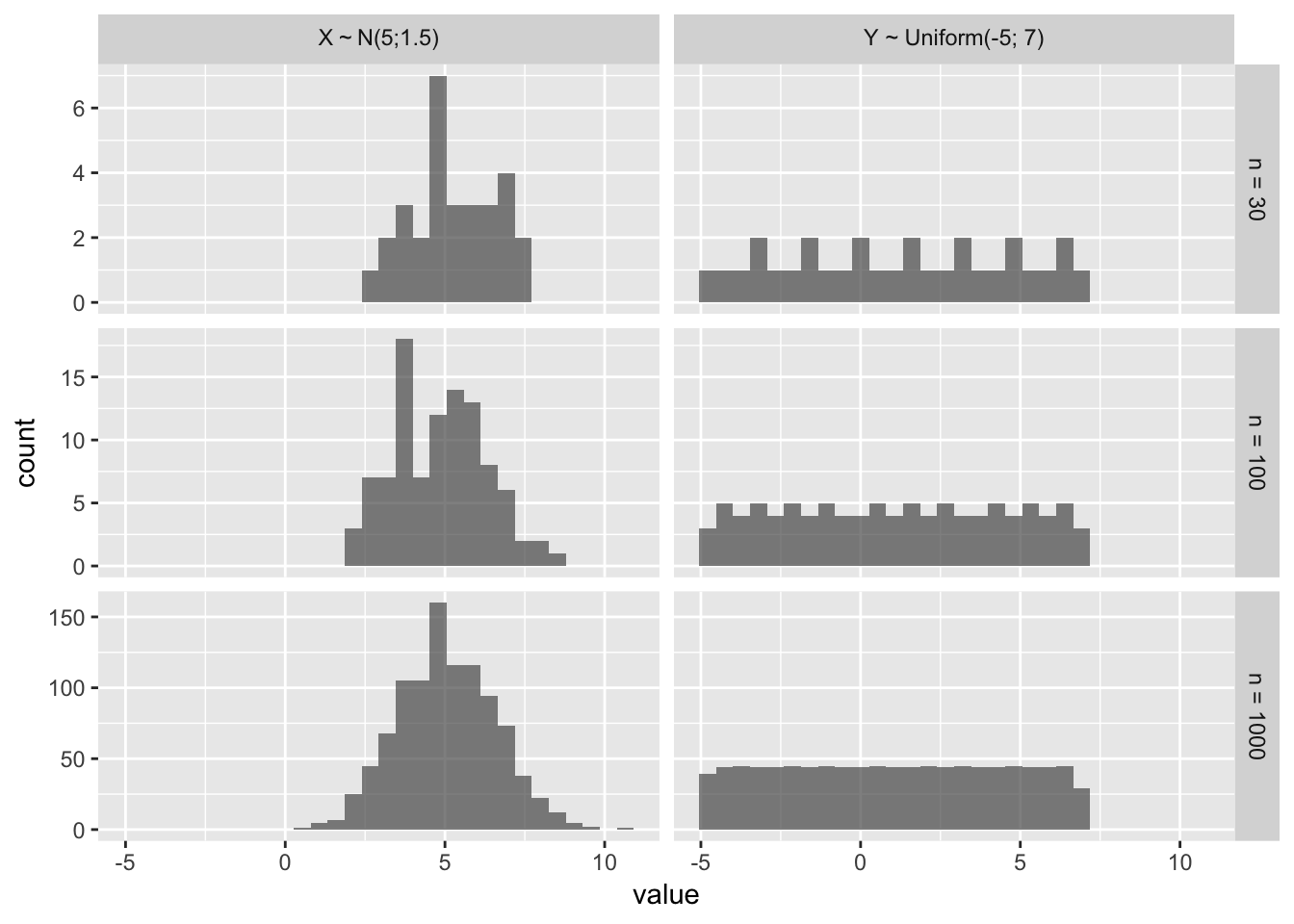
Using empirical parameters
Standard distributions
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.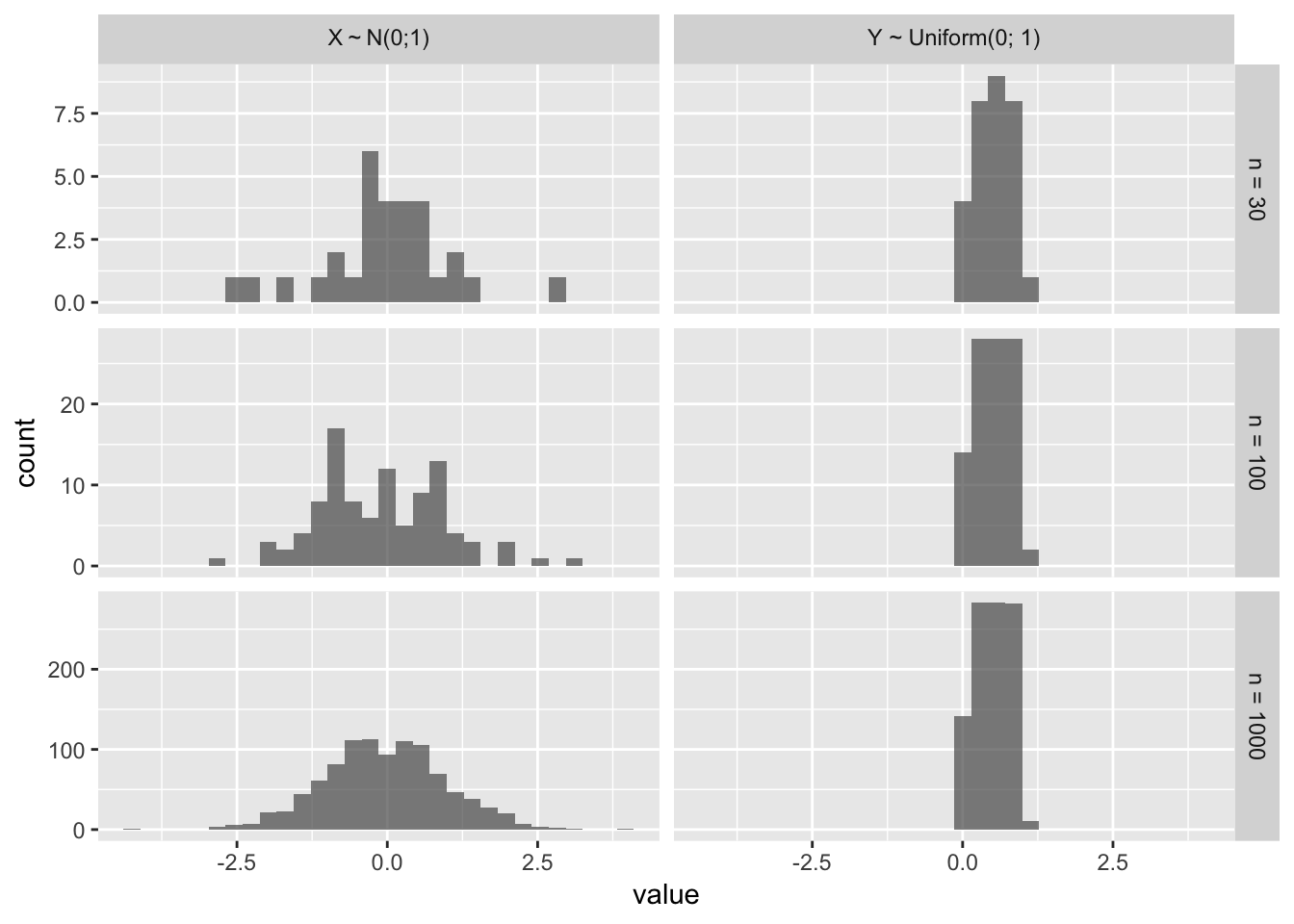
Non-standard distributions
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.