SVD of rank-deficient matrices
\[ \newcommand{\matrix}[1]{\mathbf{#1}} \] Let \(\matrix{A}\) be a data set of \(m\) points in \(\mathbb{R}^d\). One application of SVD is to create a compressed representation of \(\matrix{A}\). Rank-\(k\) approximation of \(A\) is created by calculating the singular value decomposition of \(\matrix{A}\) \[ \matrix{A} = \matrix{U}\matrix{\Sigma}{\matrix{V}} \] and reconstruct it with \(k \leq d\) first singular values. \[ \matrix{A_k} = \matrix{U_k}\matrix{\Sigma_k}\matrix{V_k^T} \]
SVD in R
Each implementation of SVD has some varieties in the output representation. For example, the right singular vectors \(\matrix{V}\) may or may not be be already transposed. In R, one can run svd(A) to obtain SVD, and get the output as below
## [,1] [,2] [,3]
## [1,] 1 6 11
## [2,] 2 7 12
## [3,] 3 8 13
## [4,] 4 9 14
## [5,] 5 10 15## $d
## [1] 3.512722e+01 2.465397e+00 1.269091e-15
##
## $u
## [,1] [,2] [,3]
## [1,] -0.3545571 0.68868664 0.57004417
## [2,] -0.3986964 0.37555453 -0.74547800
## [3,] -0.4428357 0.06242242 -0.17015793
## [4,] -0.4869750 -0.25070970 0.29657318
## [5,] -0.5311143 -0.56384181 0.04901858
##
## $v
## [,1] [,2] [,3]
## [1,] -0.2016649 -0.8903171 0.4082483
## [2,] -0.5168305 -0.2573316 -0.8164966
## [3,] -0.8319961 0.3756539 0.4082483Although \(U\) should be a squared matrix, svd(A)$u is in fact an \(m\times d\) matrix. However, this truncation does not compromise the information in \(\matrix{A}\). Since all the rows \(d+1, d+2, \dots, m\) in \(\Sigma\) are 0, one can safely remove the columns \(d+1, d+2, \dots, m\) in \(\matrix{U}\).
Reconstruction
k.approx <- function(X,k) {
X.svd = svd(X)
D = diag(X.svd$d, nrow=k)
return(X.svd$u[,1:k] %*%D %*% t(X.svd$v)[1:k,])
}A = matrix(runif(1000),nrow=50)
residuals.rand = vary.k(A)
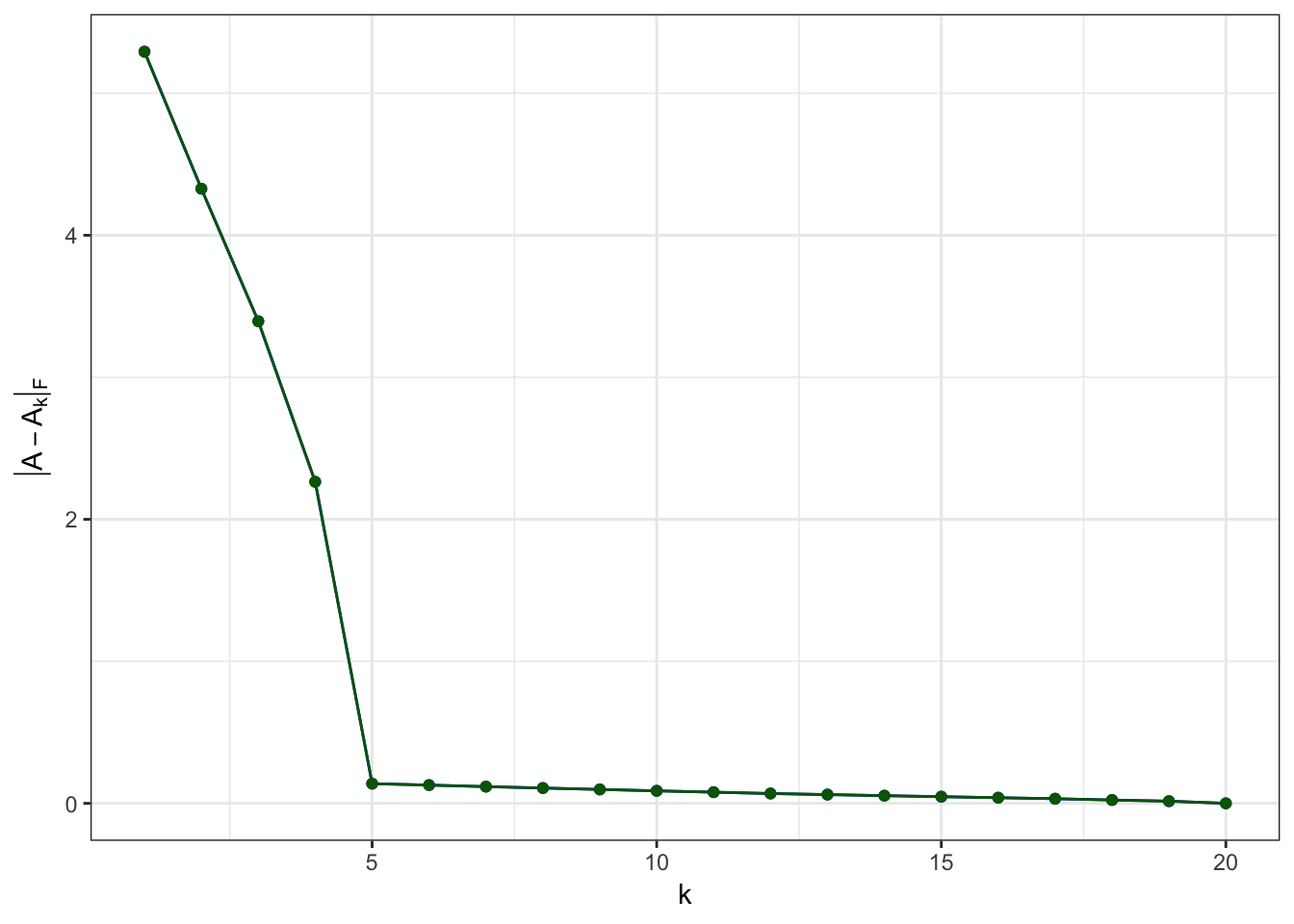
ggplot(residuals.rand,aes(x=k,y=residuals)) +
geom_line(color='blue') +
geom_point(color='blue') +
xlab(expression(k)) +
ylab(expression(group("|",A-A[k],"|")[F])) +
theme_bw()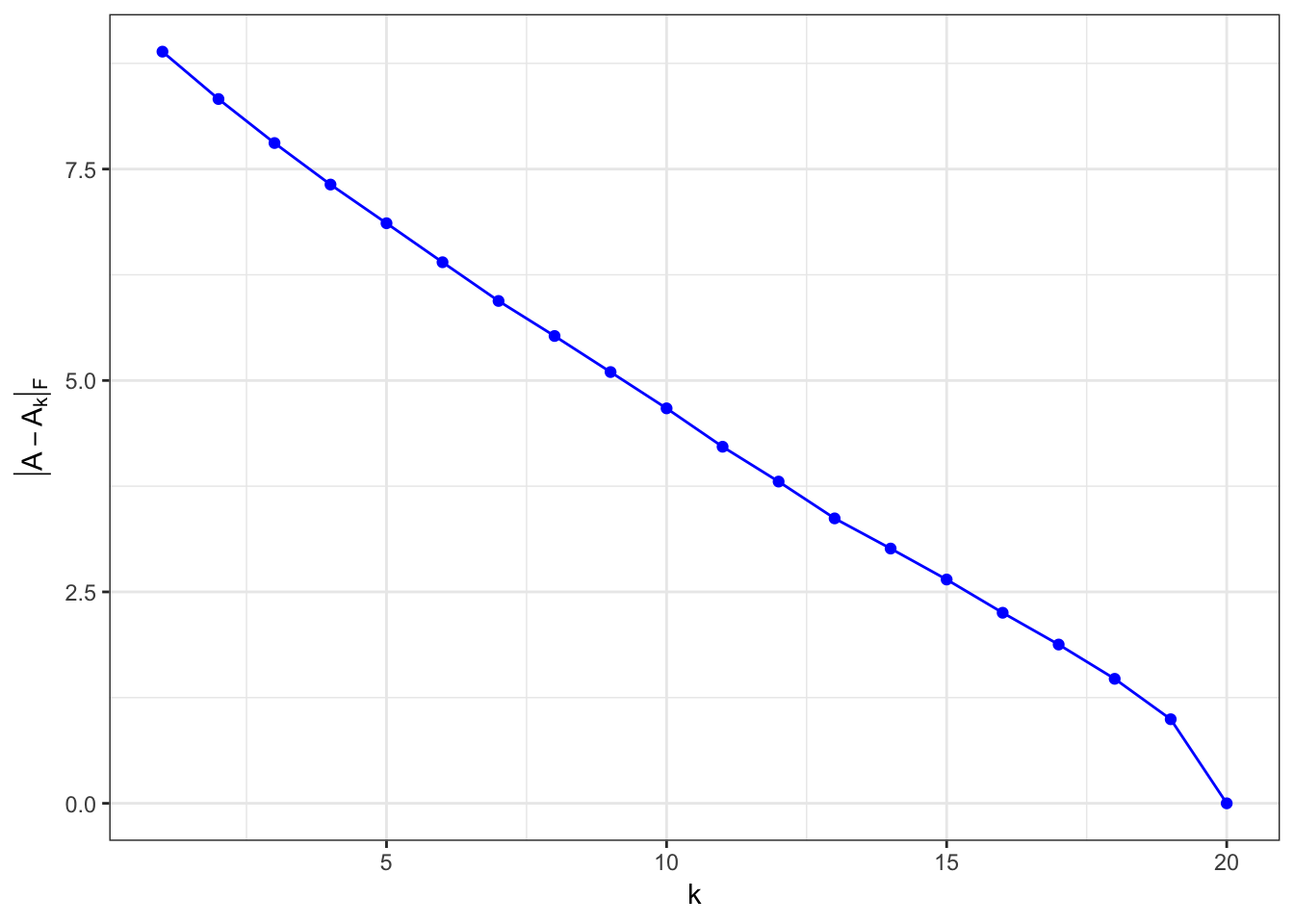
\(\matrix{A}\) is rank-1 matrix
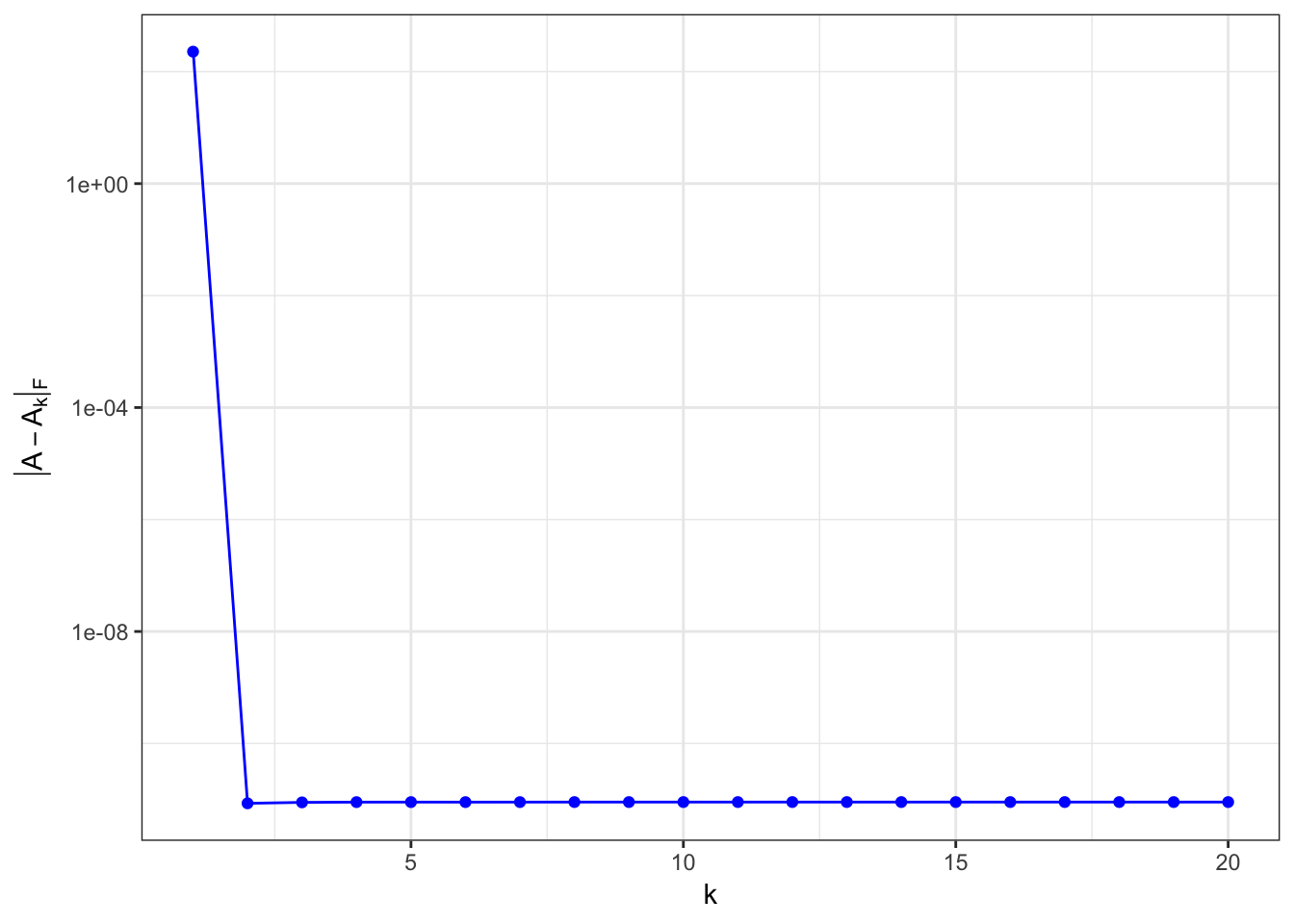
\(\matrix{A}\) is rank-5 matrix
Every column in \(\matrix{A}\) is linearly dependent on the first five columns.
A = matrix(rep(0,1000),nrow=50)
A[,1:5] = matrix(runif(nrow(A)*5),ncol=5)
for (i in 6:ncol(A)) {
A[,i] = A[,sample(5,size=1)]*runif(1) # + runif(nrow(A), min = -0.5,max=0.5)
}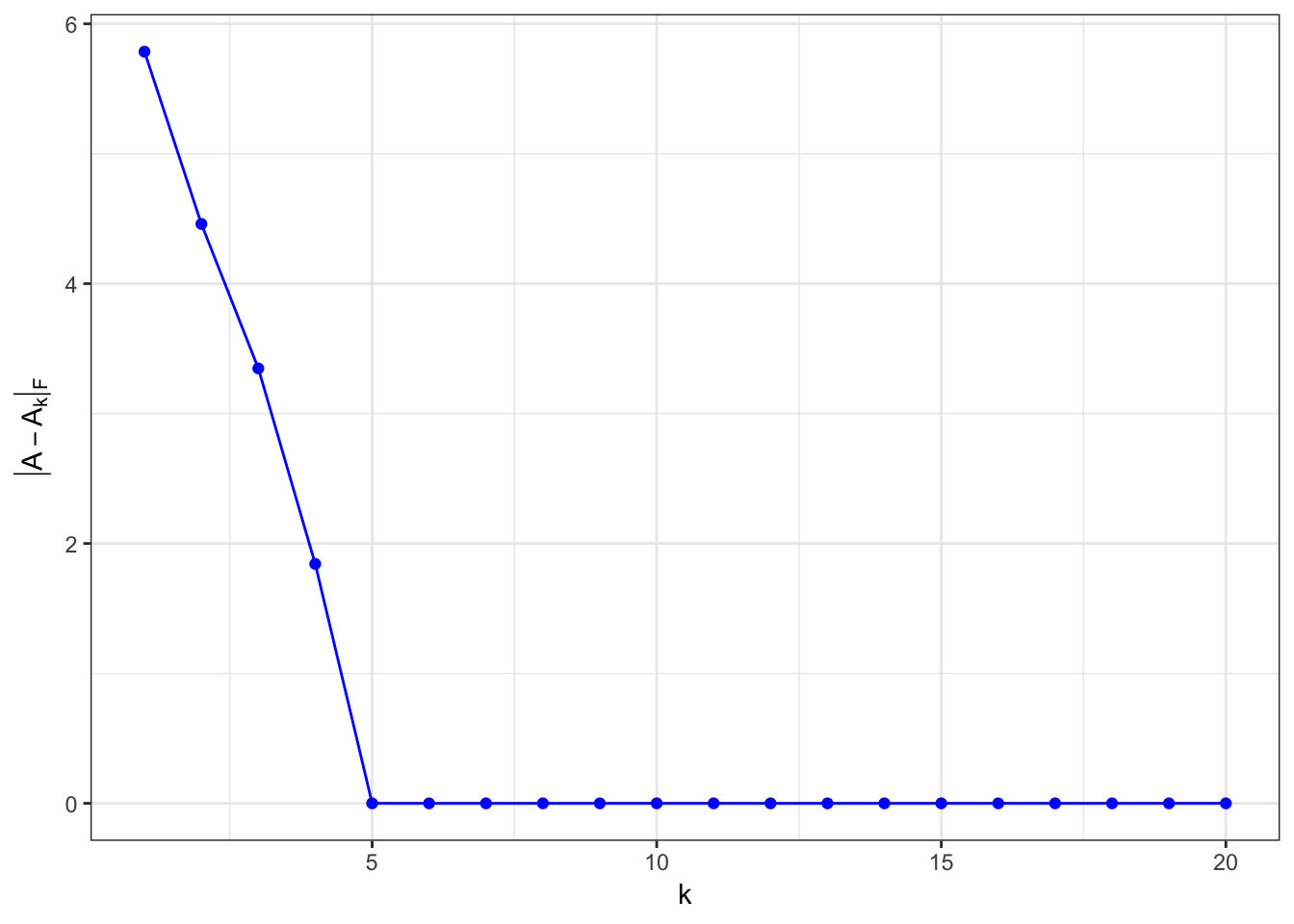
\(\matrix{A}\) is rank-5 matrix, with some noise
A = matrix(rep(0,1000),ncol=20)
A[,1:5] = matrix(runif(nrow(A)*5),ncol=5)
for (i in 6:ncol(A)) {
A[,i] = A[,sample(5,size=1)]*runif(1) + runif(nrow(A), min=-1e-2, max=1e-2) # + runif(nrow(A), min = -0.5,max=0.5)
}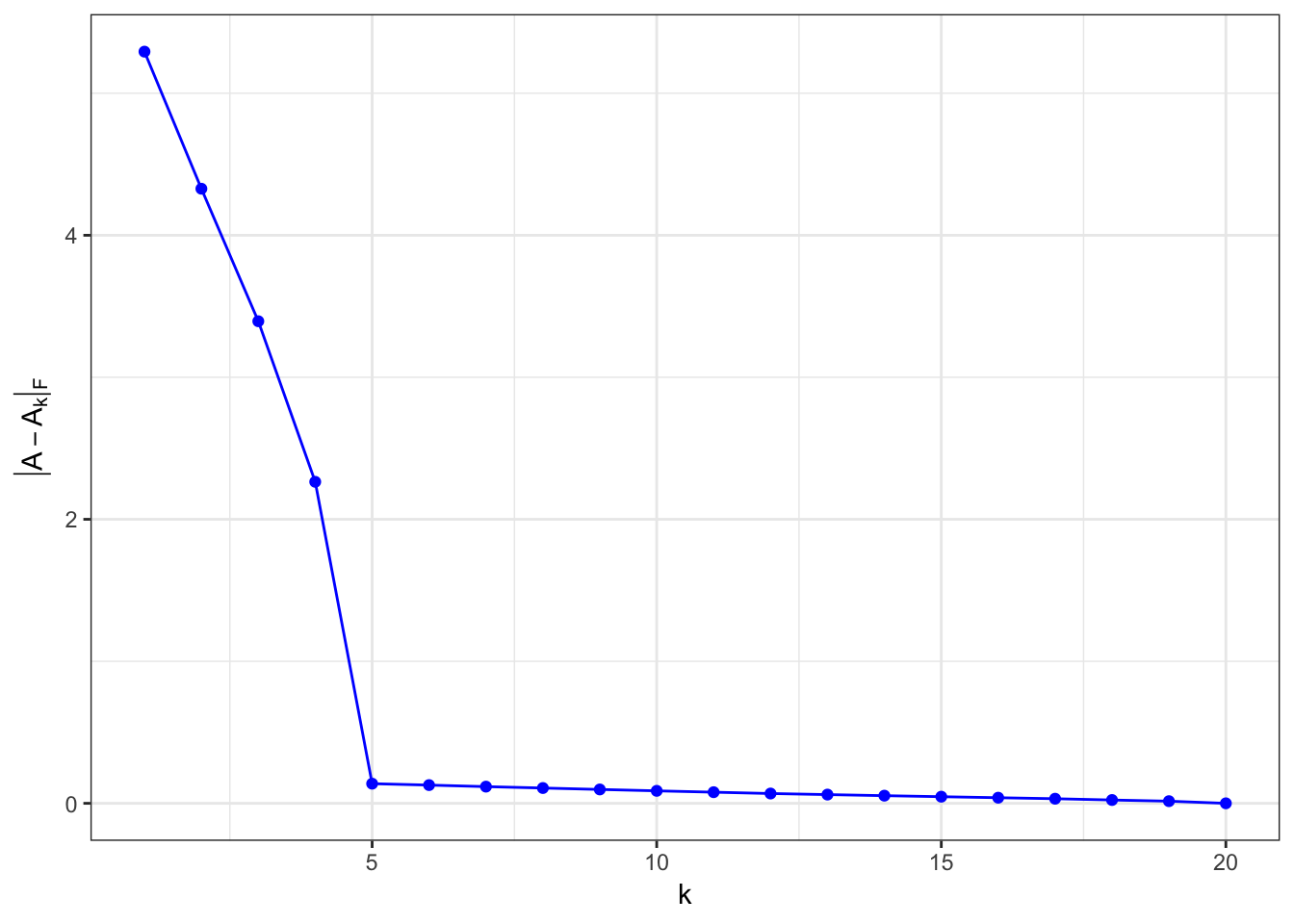
Same rank matrices with different sizes
B = matrix(rep(0,400),ncol=20)
B[,1:5] = matrix(runif(nrow(B)*5),ncol=5)
for (i in 6:ncol(B)) {
B[,i] = B[,sample(5,size=1)]*runif(1) + runif(nrow(B), min=-1e-2, max=1e-2) # + runif(nrow(A), min = -0.5,max=0.5)
}
Characteristics of singular values
Magnitude
A.svd = svd(A)
B.svd = svd(B)
sv.df = data.frame('i' = 1:length(A.svd$d),'A' = A.svd$d, 'B'= B.svd$d)
ggplot(sv.df, aes(x=i)) +
geom_line(aes(y=A), color='blue') +
geom_point(aes(y=A), color='blue') +
geom_line(aes(y=B), color='darkgreen') +
geom_point(aes(y=B), color='darkgreen') +
ylab(expression(S[i])) +
theme_bw()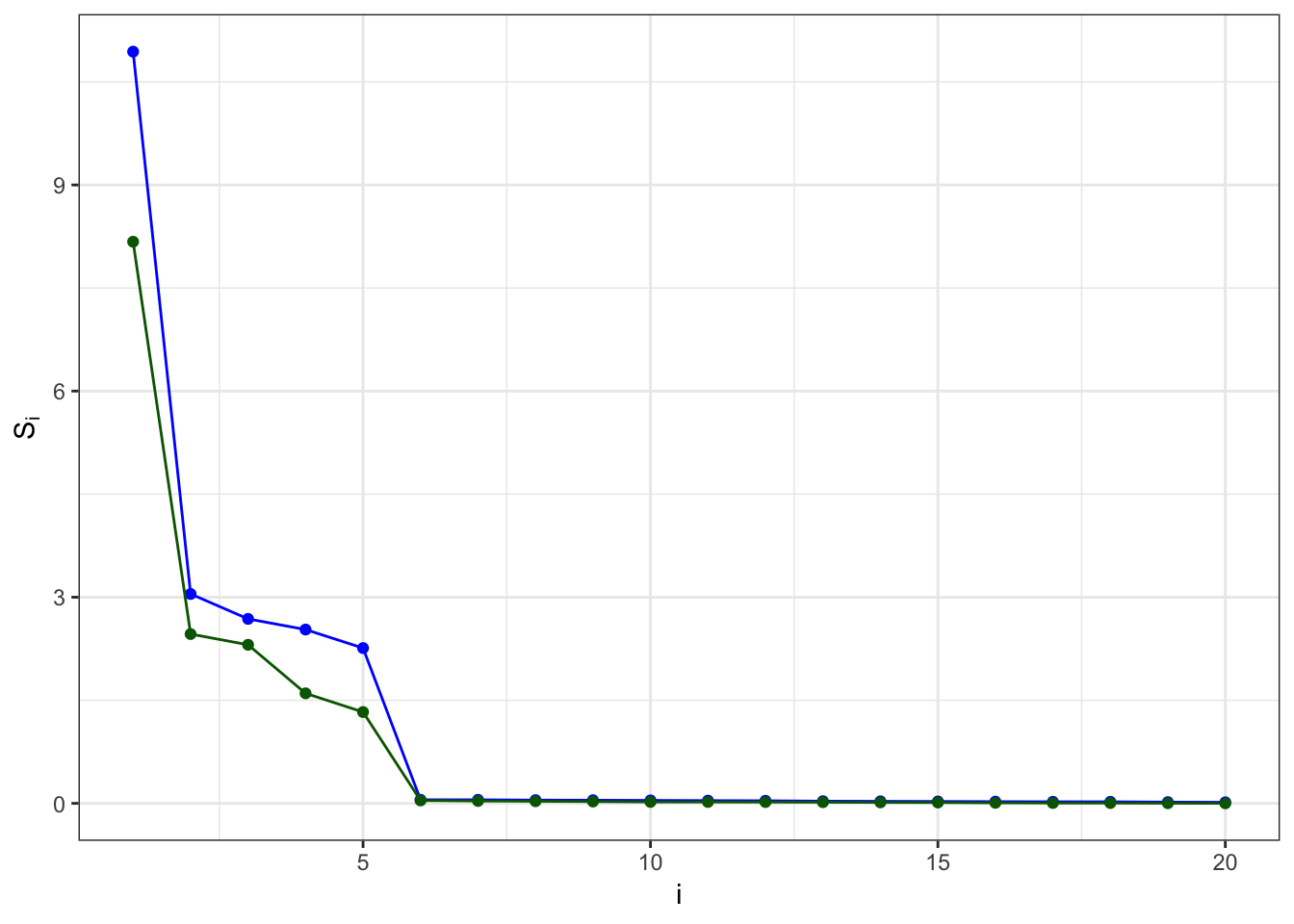
Relative contributions
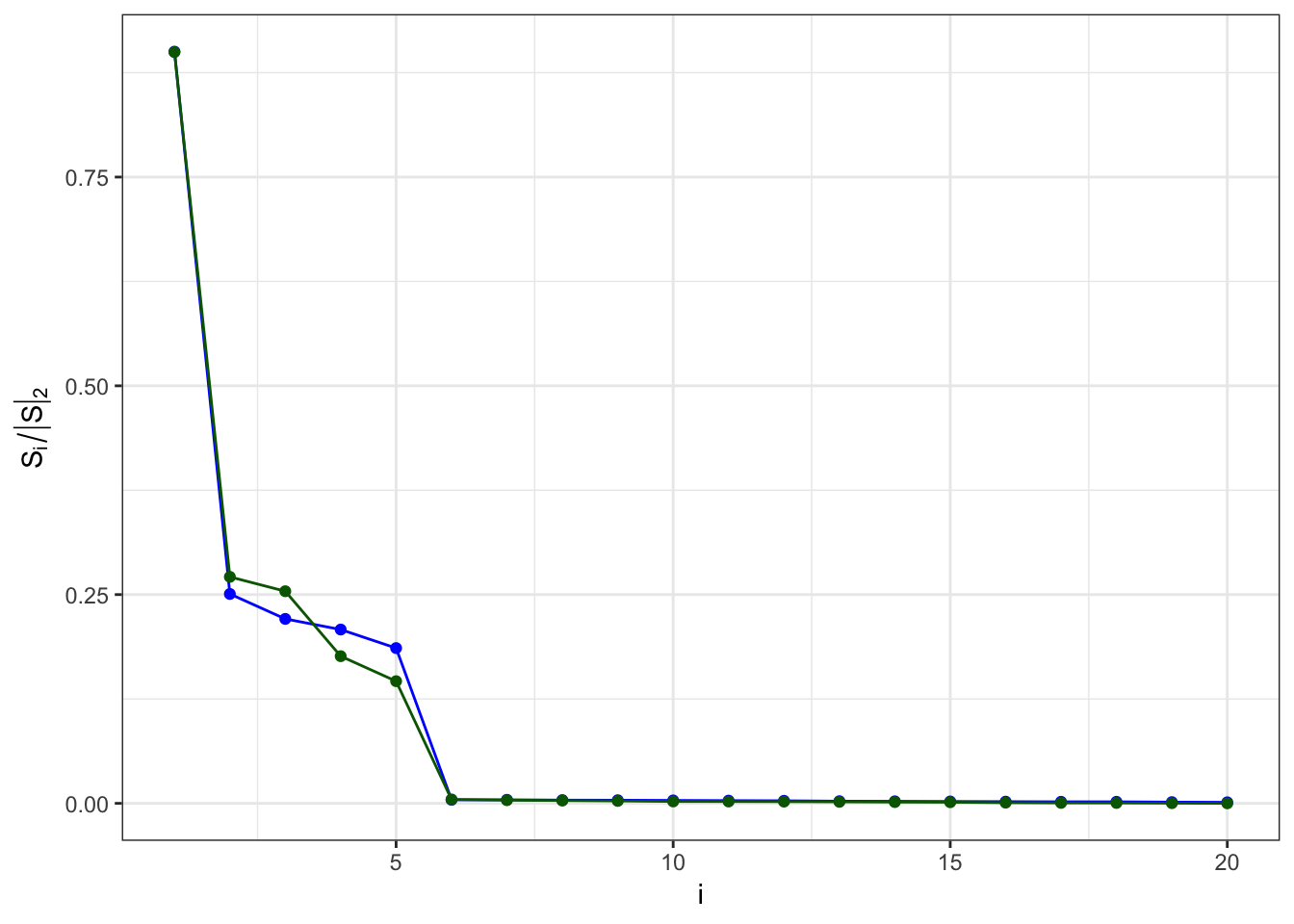
\(B = \alpha A\)
mult.sv = data.frame('i' = 1:min(dim(A)))
for (const in 10^c(0,1,2,3,4)) {
B = const * A
ABdiff = (B/ norm(B,type='F')) - (A/norm(A,type='F'))
diff.svd = svd(ABdiff)
mult.sv[,as.character(const)] = diff.svd$d
}
mm = reshape2::melt(mult.sv,id.vars='i')
mm$variable = as.numeric(as.character(mm$variable))
ggplot(mm, aes(x=i,y=value,group=factor(variable),color=variable)) +
geom_line() +
ylab(expression(S[i])) +
theme_bw()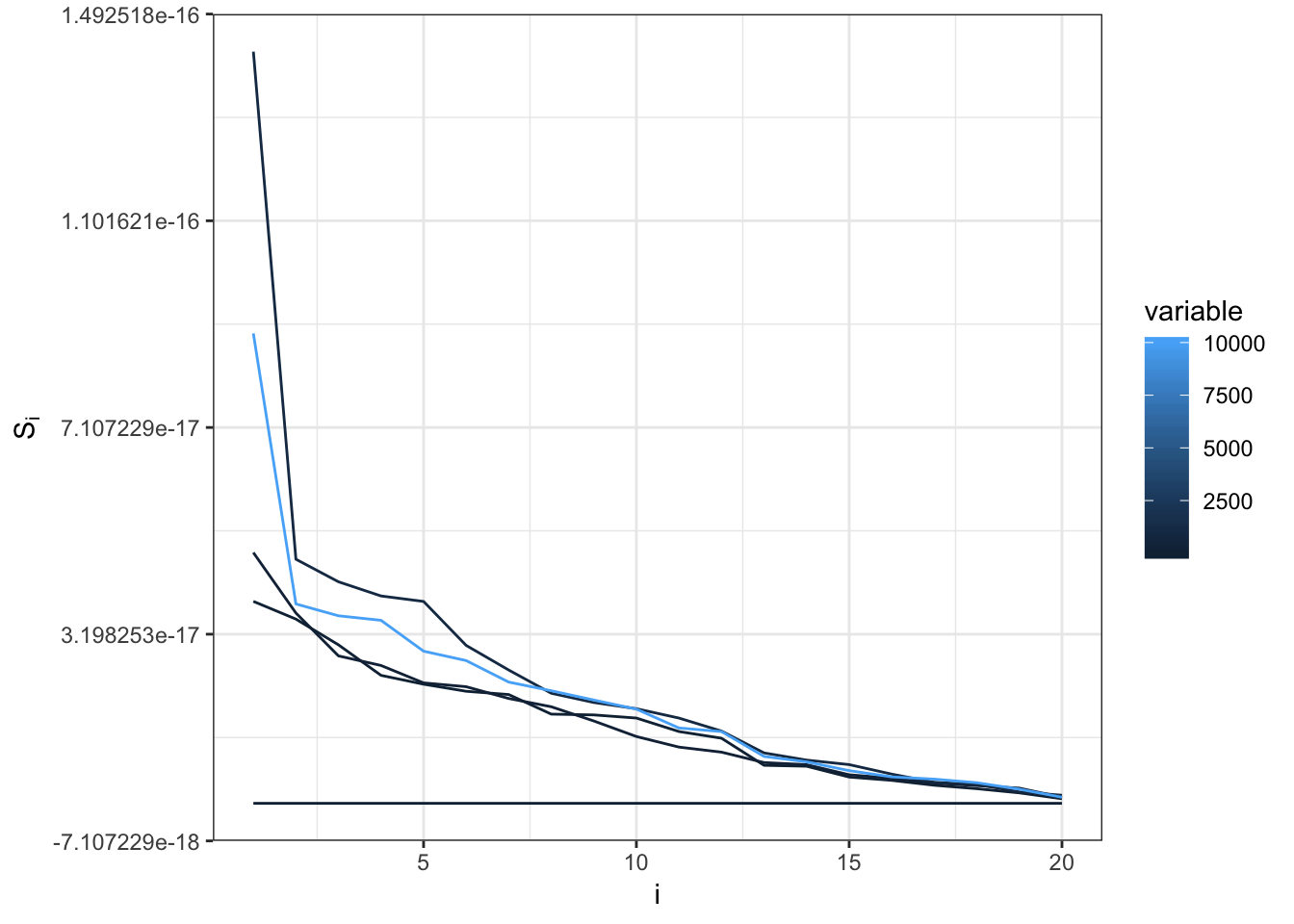
\(B = const \times A + \epsilon\)
\[\epsilon \sim Normal(0,1)\]
dXY.p <- function(X,Y, lower.tail = TRUE) {
d = svd(X-Y)$d
d = d / sum(d) # singular values are non-negative, no need to square
E.d = 1/ length(d)
# chisq = \sum(Obs_i - Exp_i)^2 / Exp_i
chisq = sum( (d - E.d)^2 / E.d)
return(pchisq(chisq, length(d) - 1,lower.tail = lower.tail))
}
mult.sv = data.frame('i' = 1:min(dim(A)))
factors = 10^c(0,1,2,3,4,5)
pVals = data.frame('MultiplicationFactor' = factors)
for (i in 1:length(factors)) {
const = factors[i]
B = const * A + rnorm(Reduce('*',dim(A)),mean = 0,sd = 0.1*const)
ABdiff = (B/ norm(B,type='F')) - (A/norm(A,type='F'))
diff.svd = svd(ABdiff)
mult.sv[,as.character(const)] = diff.svd$d
pVals[i,'p-value'] = dXY.p(A,B)
}
mm = reshape2::melt(mult.sv,id.vars='i')
names(mm) = c('rank', 'MultiplicationFactor', 'SingularValue')
mm[['MultiplicationFactor']] = as.numeric(as.character(mm$MultiplicationFactor))
ggplot(mm, aes(x=rank,y=SingularValue,group=factor(MultiplicationFactor),color=MultiplicationFactor)) +
geom_line() +
ylab(expression(S[i])) +
theme_bw()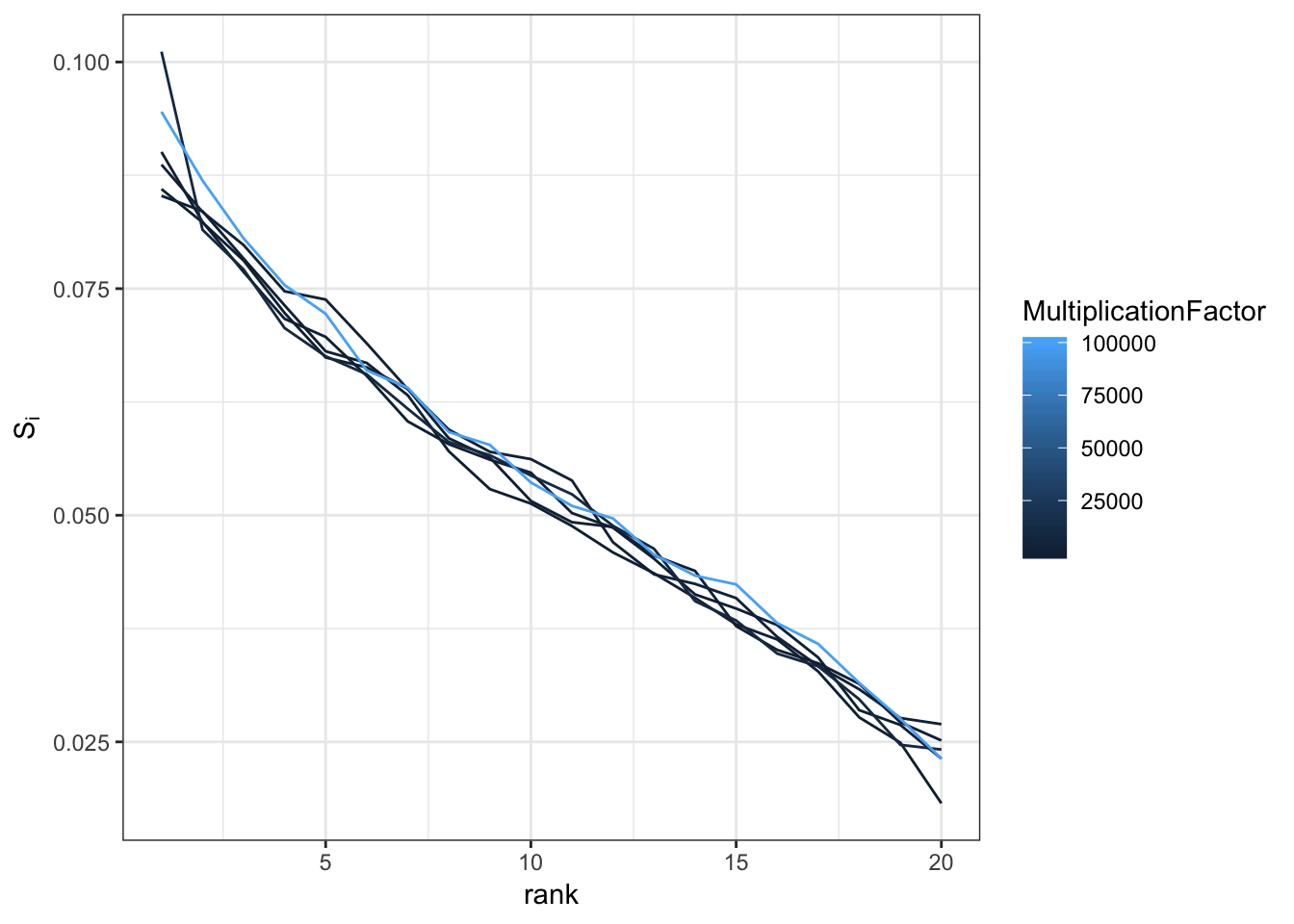
pVals## MultiplicationFactor p-value
## 1 1e+00 7.664707e-18
## 2 1e+01 3.451641e-07
## 3 1e+02 7.642776e-07
## 4 1e+03 5.246422e-07
## 5 1e+04 7.753992e-07
## 6 1e+05 5.346436e-07