kNN estimator in action
\(k^{th}\)-nearest neighbor Entropy estimator
Nearest neighbor estimator
\[ H(X) \text{(nats)} \approx -\psi(1) + \psi(N) + \frac{1}{N-1} + \ln c_d + \frac{1}{N}\sum\limits_{i=1}^{N} \ln (d_1(x_i)) \]
in which
- \(\psi(x) = \frac{\Gamma '}{\Gamma}\) is the gamma function
- \(\psi(1) = -e = -0.5772156...\) (Euler-Mascheroni constant)
- \(c_d\) is the volume of the d-dimensional unit sphere
- \(d_1(x_i)\) is the distance from \(x_i\) to its nearest neighbor
\(k^{th}\)-nearest neighbor estimator
\[ H(X) \approx -\psi(\color{red}{k}) + \psi(N) + \frac{1}{N-1} + \ln c_d + \frac{1}{N}\sum\limits_{i=1}^{N} \ln (d_{\color{red}{k}}(x_i)) \]
in which
- \(d_k(x_i)\) is the distance from \(x_i\) to its \(k^{th}\)-nearest neighbor
1D Example
The data below is generated from the Normal distribution \(X \sim N(0,1)\)
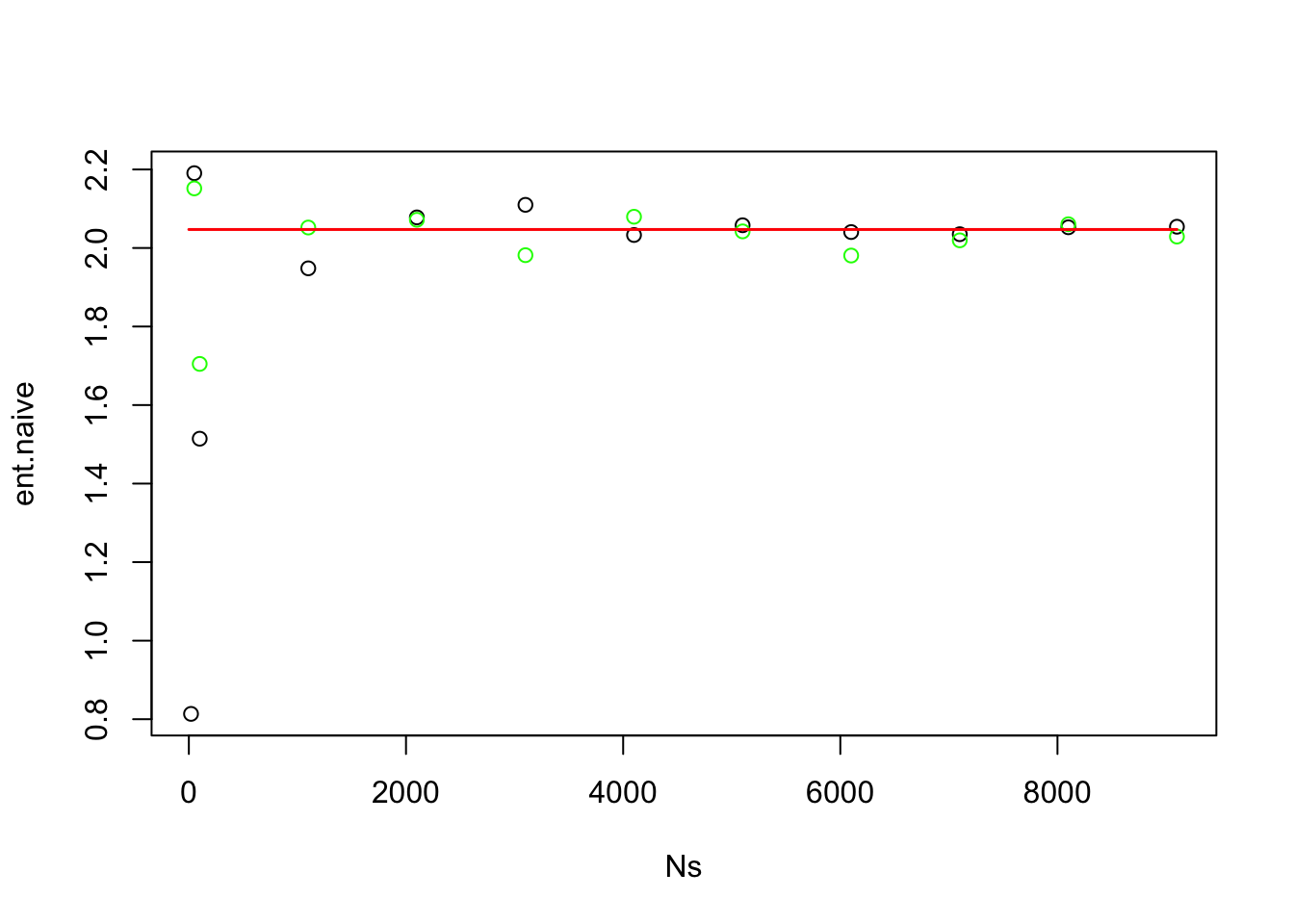
The true entropy is
\(H(X) = - \int p(x) \log p(x) dx\) = 2.0470956
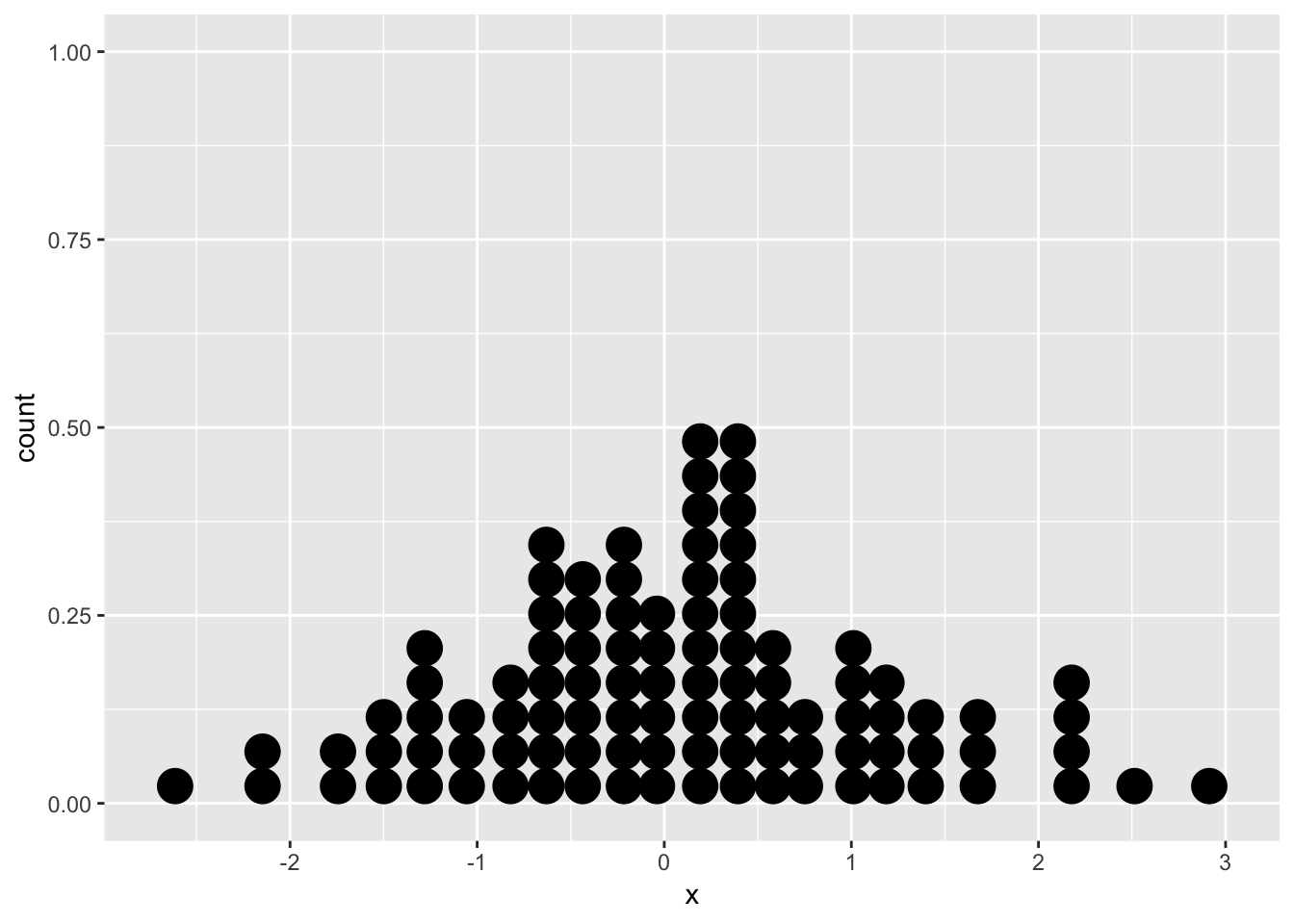
To estimate entropy using k-nearest neighbor distance, we
sort the data
Take the mean of nearest neighbor distance
Plug in the approximation
The approximation at different number of samples
\(k^{th}\)-nearest neigbor Mutual information estimator
Estimating entropy in joint space
Consider a pair of data point (X,Y) to be a data point Z in the joint space of \((d_X + d_Y)\) dimensions. The joint entropy \(H(X,Y)\) can be treated as the entropy of \(Z\) in the joint space
\[ H(X,Y) \approx -\psi(\color{red}{k}) + \psi(N) + \ln c_{d_X} c_{d_Y} + \frac{d_X + d_Y}{N}\sum\limits_{i=1}^{N} \ln (d_{\color{red}{k, XY}}(x_i)) \]
